Categories: Mechanics

Difference between elastic and inelastic collision with examples

Basically, there are two main types of collision, elastic collision, and inelastic collision. The basic difference between elastic and inelastic collision is that inelastic collision kinetic energy is conserved while in inelastic collision kinetic energy is not conserved.

What is a Collision?

In a collision, a relatively large force acts on each colliding particle for a relatively short time. The basic idea of a collision is that the motion of the colliding particles (or of at least one of them) changes rather abruptly and that we can make a relatively clean separation of time that are “before the collision” and those that are “after the collision”.

When a bat strikes a baseball, for example, the beginning and the end of the collision can be determined fairly precisely. The bat is in contact with the ball for an interval that is quite short compared with the time during which we are watching the ball. During the collision, the bat exerts a large force on the ball. This force varies with time in a complex way that we can measure only with difficulty. Both the ball and the bat are deformed during the collision. Forces that act for a time that is short compared with the time of observation of the system are called impulsive forces.

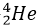
When an alpha particle ( HELIUM HELIUM nucleus) collides with another nucleus, the force acting between them may be the well-known repulsive electrostatic force associated with the charges on the particles. The particles may not actually touch, but we still may speak of a collision because a relatively strong force, acting for a time that is short compared with the time that the alpha particle is under observation, has a substantial effect on the motion of the alpha particle.

We can even speak about a collision between two galaxies if we were prepared to observe then over a time skill of the order of millions or billions of years. (But a more feasible alternative is to shorten this long time span by computer modeling).

The collision between elementary particles provide the principal source of information about there internal structure. When two particles collide and high energy, often the products of the collision are very different from the original particles. Some times these collisions produce hundreds of product particles whose total mass may be far greater than the masses of colliding particles ( Kinetic energy of the incident particles being converted into rest energy in the collision). By studying the trajectories of the outgoing particles and applying the fundamental conservation laws, we can reconstruct the original event.

On a different scale, those who study traffic accidents also try to reconstruct collisions. Form the paths and impact patterns of the colliding vehicles, it is often possible to deduce such important details as the speed and direction of motion of the two vehicles before the collisions.

Another kind of collision is one that takes place between a space probe and a planet” called the sling short effect”, In which the speed and the direction of space probe can be altered in a “close encounter” with a moving planet. The probe does not actually touch the planet, but it does come strongly under its gravitational influence for a time that is very short compared to the direction of the space prob’s journey. Thus we are justified in calling such in counters “collisions”.

Is momentum is conserved inelastic Collision?

“The momentum of an isolated system of two or more interacting bodies remains constant”.

The momentum of a system depends on its mass and velocity. A system is a group of bodies within certain boundaries. An Isolated System is a group of interacting bodies on which no external force is acting. If no unbalanced or net force acts on a system, its momentum remains constant. Thus the momentum of an isolated system is always conserved. This is the Law of Conservation of Momentum.

Consider the example of an air-filled balloon as described under the third law of motion. In this case, balloon and the air inside it form a system. Before releasing the balloon, the system was at rest and hence the initial momentum of the system was zero. As soon as the balloon is set free, air escapes out of it with some velocity. The air coming out of it processes momentum. To conserve momentum, the balloon moves in a direction opposite to that of air rushing out.

Consider an isolated system of two spheres of masses m ₁and m ₂. They are moving in a straight line with initial velocities u₁ and u₂respectively, but that u₁is greater than u_{2. The sphere} of mass m₁approaches the sphere of mass m₂as they move.

The initial momentum of mass m₁= m₁ u₁

The initial momentum of mass m₂=m₂ u₂

The total initial momentum of the system before collision=m₁ u₁+ m₂ u₂……….(1)

After sometime mass m₁ hits mass m₂ with some force. According to Newton’s third law of motion,m₂ exerts an equal and opposite reaction force on m₁. Let their velocities become v₁ and v₂ respectively after collision. then:

Final momentum of mass m₁=m₁v₁

Final momentum of mass m₂ =m₂v₂

Total momentum of the system after collision =m₁v₁+ m₂v₂……..(2)

According to the law of conservation of momentum:

The total initial momentum of the system before collision = Total final momentum of the system after the collision

m₁ u₁+ m₂₌m₁v₁+ m₂v_{2 ……………………(3)}

Equation (3) shows that the momentum of an isolated system before and after collisions remains the same which is the law of conservation of momentum. The law of conservation of momentum is an important law and has vast applications.

Collision in one dimension

We consider the effect of a collision between two objects. Usually, we know the initial velocities of the two objects before the collision, and our goal is to apply conservation laws or laws of motion to find the velocities after the collision.

We can always calculate the motions of objects after they collide from their previous motions if we know the forces that act during the collision and if we can solve the equation of motion. In most collisions, however, we do not know these forces. The Law of Conservation of momentum must hold during any collision in which only internal forces act, and it can be applied even if we do not know the forces. Although we may not know the details of the interaction, we can use the conservation of momentum and the conservation of energy in many cases to predict the results of the collision.

Linear momentum is always observed in collisions. The total energy is also conserved: the initial total energy of the colliding particles is equal to the final total energy of the products. This energy may include not only kinetic energy but other forms as well, such as internal energy, the energy of deformation, rotational energy, radiant energy, and so on.

In one special category of collision, called an elastic collision, we neglect all these other forms of energy and consider, we neglect all these other forms of energy and consider only mechanical energy U + K. Furthermore, we assume that in an impulsive collision, the internal forces act for a short time and therefore over a short distance; we observe the particles only at much greater relative separation, so that the effects of their interval potential energy can be neglected. In an elastic collision, translational kinetic energy in the only form of energy that we must account for, and conservation of mechanical energy is therefore equivalent to conservation of kinetic energy: the initial energy K_iequals the final kinetic energy K_f in an elastic collision.

In another category of the collision, which is called inelastic, energy appears in other forms, and the initial final kinetic energies are not equal. In some cases, K_i_>K_f , as, for example, when initial kinetic energy is converted into internal energy of the products, while in other cases K_i_>K_{f ,}such as when internal energy stored in the colliding particles is released. Mechanical energy U +K is not conserved in an inelastic collision.

When the colliding bodies are simple, such as atoms or molecules, we can often account directly for the difference between K_iand K_f in terms of the known discrete internal energy states of the system.In more complex systems, such as colliding automobiles, we regard the difference simply as “lost” or “gained” kinetic energy.

All collisions between real objects are to some extent inelastic. When the objects are very rigid, such as billiard balls, we can often treat the collision as approximately elastic. In this case, the energy that is changed from kinetic to other forms (such as the sound wave you hear when the balls collide) is negligible compared with the kinetic energy. Note that the classification of a collision as elastic or inelastic is independent of the reference frame from which the collision is viewed.

When the two bodies stick together after the collision, the collision is said to be completely inelastic. For example, the collision between a bullet and a block of wood into which is fired is completely inelastic when the bullet remains embedded in the block. The term completely inelastic does not necessarily mean that all the initial kinetic energy is lost; as we shall see, it means rather than the loss is a large as it can be, consistent with momentum conservation.

Even if the forces of a collision are not known, we can find the motions of the particles after collision from the motions before collision, provided the collision is completely inelastic, or, if the collision is elastic, provided the collision takes place in one dimension. For a one dimensional collision the relative motion after the collision is along the same line as the relative motion before the collision. We restrict ourselves to one-dimensional motion for the present.

Difference between elastic and inelastic collision

In the forces between the bodies are also conservative, so that no mechanical energy is lost or gained in the collision, the total kinetic energy of the system is the same after the collision as before. Such a collision is called an elastic collision. A collision between two marbles or two billiard balls is almost completely elastic. When the gliders collide, their springs are momentarily compressed and some of the original kinetic energy is momentarily converted to elastic potential energy. Then the gliders bounce apart, the springs expand, and this potential energy is converted back to its kinetic energy.

A collision in which the total kinetic energy after the collision is less than before the collision is called an inelastic collision. A meatball landing on a plate of spaghetti and a bullet embedding itself in a block of wood are examples of inelastic collisions. An inelastic collision in which the colliding bodies stick together and move as one body after the collision is often called a completely inelastic collision Inelastic Collisions:

inelastic collision formula

Lets’ s look at what happens to momentum and kinetic energy is a completely inelastic collision of two bodies (A and B). Because the two bodies stick together after the collision, they have the same final velocity V^→2.

Suppose, for example, that a body with mass m_Aand initial x-component of velocity ν _A1xcollides inelastically with a body with mass m_Bthat is initially at rest (ν _B1x= 0). From Eq.(1) the common x-component of velocity ν _2x of both bodies after the collision is:

The right side is always less than unity because the denominator is always greater than the numerator. Even when the initial velocity of m_Bis not zero, it is not hard to verify that the kinetic energy after a completely inelastic collision is always less than before.

Please note: We don’t recommend memorizing Eqs. (2) or (3). We derived them only to prove that kinetic energy is always lost in a completely inelastic collision.

Elastic Collision formula

We saw in section, that an elastic collision in an isolated system is one in which kinetic energy (as well as momentum) is conserved. The elastic collision occurs when the forces between the colliding bodies are conservative. When two billiard balls collide, they squash a little near the surface of contact, but then they spring back,but at the end, it is reconverted to kinetic energy.

Let’s look at an elastic collision between two bodies A and B. We start with a one-dimensional collision, in which all the velocities lie along the same line; we choose this line to be the x-axis. Each momentum and velocity then has only an x-component. We call the x-velocities before the collision ν _A1x and ν _B1x , and those after the collision ν _A2x and ν _b2x . from conservation of kinetic energy we have:

And conservation of momentum gives
m_Aν _A1x + m_Bν _B1x = m_Aν _A2x+ m_Bν _B2x
If the masses m_A and m_Band the initial velocities ν _A1x and ν _B1x are known, we can solve these two equations to find the two final velocities ν _A2xand ν _B2x .

Inelastic collision examples

Elastic collisions One Body initially at Rest

The general solution to the above equation is a little complicated, so we will concentrate on the particular case in which body B is at rest before the collision (so ν _B1x = 0). Think of body B as a target for body A to hit. Then the kinetic energy and momentum conservation equation is, respectively.

we can solve for ν _A2x and ν _B2xin terms of the masses and the initial velocity ν _A1x . This involves some fairly strenuous algebra, but it’s worth it. No pain, no gain! The simplest approach is somewhat indirect, but along the way, it uncovers an additional interesting feature of elastic collisions.

Now we can interpret the result. Suppose body A is a Ping-Pong ball and body B is a bowling ball. Then we expect A to bounce off after the collision with a velocity nearly equal to its original value but in the opposite direction, and we expect B’s velocity to be much less. That’s just what the equations predict. when m_Ais much smaller than m_B, the fraction in Eq.(9) is approximately equal to (-1),so ν _A2x. The fraction in Eq.(10) is much smaller than unity, so ν _B2xis much less than ν _A1x. The opposite case,in which A in the bowling ball and B the Ping-Pong ball and m_Ais much larger than m_B. What do you expect to happen than? Check your predictions against Eq.(9) and (10).

Another interesting case occurs when the masses are equal. If m_A= m_B,then Eqs.(9) and (10) give ν _A2x = 0 and ν _B2x = ν _A1x . That is, the body that was moving stops dead; it gives all its momentum and kinetic energy to the body that was at rest. This behavior is familiar to all pool players.

Elastic Collisions and Relative Velocity

Let’s return to the more general case in which A and B have different masses. Equations (8) can be written as
ν _A1x = ν _B2x– ν _A2x …………….(11)

Here ν _B2x– ν _{A2x is}the velocity of B relative to A after the collision; from Eq.(11) this equals ν _A1x , which is the negative of the velocity of B relative to A before the collision. The relative velocity has the same magnitude, but opposite sign, before and after the collision. The sign changes because A and B are approaching each other before the collision but moving apart after the collision. If we view this collision from a second coordinate system moving with constant velocity relative to the first, the velocities of the bodies are different but the relative velocities are the same. Hence our statement about relative velocities holds for any straight-line elastic collision, even when neither body is at rest initially. In a straight line elastic collision of two bodies, the relative velocities before and after the collision have the same magnitude but opposite sign. This means that if B is moving before the collision,Eq.(11) becomes.

ν _B2x – ν _A2x = – (ν _B1x – ν _A1x ) ………….(12)

It turns out that a vector relationship similar to Eq.(12) is a general property of all elastic collisions, even when both bodies are moving initially and the velocities do not all lie along the same line. This result provides an alternative and equivalent definition of an elastic collision: the relative velocity of the two bodies has the same magnitude before and after the collision. Whenever this condition is satisfied, the total kinetic energy is also conserved.

When an elastic two-body collision isn’t head-on, the velocities don’t all lie along a single line. If they all lie in a plane, then each final velocity has two unknown components, and there are four unknowns in all. Conservation energy and conservation of the x- and y-components of momentum give only three equations. To determine the final velocities uniquely, we need additional information, such as the direction or magnitude of one of the final velocities.

Related Comparison Topics:

Difference between AM and FM	Conductors Vs Insulators
AC vs DC	AC MOTOR vs DC MOTOR
Center of mass Vs Center of Gravity	Interference Vs Diffraction
Electric field Vs Electric field Intensity	Force Vs Pressure
Nuclear Fission Vs Nuclear Fusion	Difference b/w free and forced oscillation