The difference between angular velocity and tangential velocity is that “The angular displacement covered by a body in unit time is called angular velocity and tangential velocity is the velocity, which is tangent to the circular path.”
Now!
We learn in detail about these quantities in an easy way. Keep reading…
Angular velocity
“Time rate of change of angular displacement is known as angular velocity.”It is denoted by ω, its formula is given by:
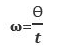
The unit of angular velocity is
- radian per second ( S.I unit)
- Degree per second ( B.E System )
- Revolution per second
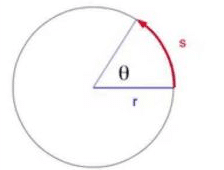
Very often we are interested in knowing how fast or how slow a body is rotating. It is determined by its angular velocity which is defined as the rate at which the angular displacement is changing with time. If Δθ is the angular displacement during the time interval Δt, the average angular velocity ωav during this interval is given by:
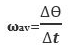
The instantaneous angular velocity ω is the limit of the ratio Δθ/Δt as Δt, following instant t, approaches zero.
Thus:
![]()
In the limit when Δt approaches zero, the angular displacement would be infinitesimally small. So it would be a vector quantity. Its direction is along the axis of rotation and is given by the right-hand rule.
See Also: Difference b/w Speed & Velocity
Types of angular velocity
Average angular velocity
“Total rate of change of angular displacement is called average angular velocity.”
Uniform angular velocity
“If the rate of change of angular displacement is constant is called uniform angular velocity.”
Non-uniform angular velocity
“If the rate of change of angular displacement is not constant is called non-uniform angular velocity.”
Instantaneously angular velocity
“Angular velocity at a particular instant of time is called instantaneous angular velocity.”
Tangential velocity
Tangential velocity is the velocity, which is tangent to the circular path. Its mathematical form is expressed as:
Vt = rω
Let’s see video now:
Related Topics:
