Work energy theorem: Equation & Examples

This is a complete post on the Topic Work Energy theorem Equation in 2020.
So if you want to get benefits from this topic, you’ll love this Post.
Let’s Dive right in….
Content …

• Definition …..
• Derivation…..
• Equation…
• Examples…
• Lot more…

Keep reading…

What is Work Energy theorem?

Work energy theorem states that: “The net work done by the forces acting on the body is equal to the change in kinetic energy of the body.” It is Also known as the principle of work and kinetic energy. Mathematically it is expressed as:

W_net = K_f –K_i = ∆k

An unbalanced force applied to a particle will certainly change the particle’s state of motion. Newton’s second law provides us with one way to analyze this change of motion. We now consider a different approach that ultimately gives the same result as Newton’s laws but is often simpler to apply. It also leads us into one of the many important conservation laws that play such an important role in our interpretation of physical processes.

Work energy theorem Equation

We consider not the work done on a particle by a single force, but the net  work W_net done by all the forces that act on the particle. There are two ways to find the net work. The first is to find the net force, that is, the vector sum of all the forces that act on the particle:

F_net=F₁+F₂+F₃+……..(1)

And then treat this net force as a single force in calculating the work according to the equation:

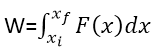
We know that a net unbalanced force applied to a particle will change its state of motion by accelerating it,let us say from initial velocity v_i to final velocity v_f. What is the effect of the work done on the particle by this net unbalanced force?
We first look at the answer to this question in the case of the constant force in one dimension. Under the influence of this force, the particles move from x_i to x_f , and it accelerates uniformly from v_i to v_f. The work done is:
W_net=F_net(x_f-x_i)=ma(x_f –x_i)
Because the acceleration is constant,we can use the equation:

to obtain:

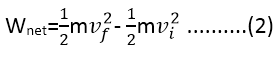
That is, the result of the net work on the particle has to bring about a change in the value of the quantity from the point I to point f. This quantity is called the kinetic energy k of the particle, with a definition

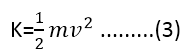
In terms of the kinetic energy k, we can rewrite equation (2) as:

                                    W_net=K_f –K_i=∆k ……….(4)

Equation (4)  is the mathematical representation of an important result called the work-energy theorem, which in words can be stated as follows:

The net work done by the forces acting on a particle is equal to the change in the kinetic energy of the particle. The work-energy theorem is useful, however, for solving problems in which the net work is done on a particle by external forces is easily computed and in which we are interested in finding the particle’s speed at certain positions.Of even more significance is the work-energy theorem as a starting point for a broad generalization of the concept of energy and how energy can be stored or shared among the parts of a complex system. The principle of conservation of energy is the subject of the next chapter.

See Also: Difference between electric potential and Electric potential energy

General proof of the Principle work and Energy

If a non-constant force acts on the object in one dimension, then the work done by the force on the object can find out by using the expression:

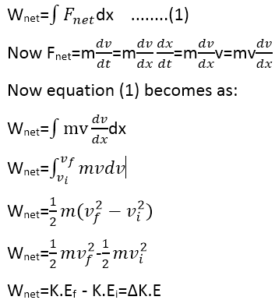
This is the expression of kinetic energy for the object under the action of the non-constant force.

What are Limitations of work energy theorem?

We derived the work-energy theorem directly from Newton’s second law, which, in the form in which we have stated it, applies only to particles. Hence the work-energy theorem, as we have presented so far, likewise applies only to particles. We can apply this important theorem to real objects only if those objects behave like particles. Previously, we considered an object to behave like a particle if all parts of the object move in exactly the same way. In the use of a work-energy theorem, we can treat an extended object as a particle if the only kind of energy it has is directed kinetic energy.

Consider, for example, a test car that is crashed head-on into a heavy, rigid concrete barrier. The directed kinetic energy of the car certainly decreases as the car hits the barrier, crumples up, and comes to rest. However, there are forms of energy other than directed kinetic energy that enters in this situation.

There is internal energy associated with the bending and crumpling of the body of the car; some of this internal energy may appear, for instance as an increase in the temperature of the car, and some may be transferred to the surroundings as heat. Note that, even though the barrier may exert a large force on the car during the crash, the force does no work because the point of application of the force on the car does not move.

 Watch also video: Stay tuned with oxscience.com

Related topics in our website are:

• Potential energy with examples
• Kinetic energy Formula 
• Energy and its types
• Energy conservation principle