Explanation of limit Calculus and Techniques to solve it:

Explanation of limit Calculus and Techniques to solve it:
Limit calculus is a branch of calculus that deals with the study of the behavior of functions as the input variable approaches a certain value or infinity. In other words, it involves the solution of the limits of functions, which are a necessary concept in calculus.
The concept of limits is used to describe the behavior of functions near a particular point, and it is fundamental in the development of derivatives, integrals, and other concepts in calculus. Limit calculus determines the limit of a function, which can do using various techniques such as algebraic manipulation, factoring, and the use of L’Hopital’s rule.
The study of limit calculus is important in many fields of science and engineering, and it has practical applications in the analysis of physical phenomena and the development of mathematical models such as the solution of differential equations.
In this article, we will discuss the definition of limit, techniques to solve the limit, applications of limits, and solving different examples to understand the concept of limits.
Definition of Limits:
The limit of a function F(x) as x approaches to “b” is “K” (where “k” may be a real number or infinity). The limit of the function is denoted as.
Lim x→b F(x) = K
If we can make the values of F(x) arbitrarily close to “K” by making x sufficiently close to “b” (but not equal to b). This means that the value of F(x) gets arbitrarily close to “K” as x approaches “b”, but it may not necessarily equal “K”. The concept of limits is important for understanding continuity, derivatives, integrals, and many more concepts in calculus analysis.
Epsilon-delta definition of Limit:
For any positive number ε, there exists a positive number δ such that,
If |x – b| < δ, then |F(x) – K| < ε
In this definition, ε represents a positive number that specifies how the function values are near to the limiting value “K” of the function. The “δ” represents a positive number that suggests how the input value close to “x” to “b” are in order for the function values with “ε” of the limit “K”.
Techniques to solve limits:
In this section, we discuss several techniques that can be used to solve the limits of functions.
- Direct substitution: If the function is continuous at the point being approached, then the limiting value find by directly putting the value of the limit into the function.
- Factoring and simplification: Algebraic manipulation of the function can help simplify the expression and make it easier to evaluate the limit. This may involve factoring, canceling or combining terms.
- L’Hopital’s rule: L’Hopital’s rule can be used to evaluate limits of indeterminate forms such as 0/0 or ꝏ/ꝏ. It involves taking the derivative of the numerator and denominator and evaluating the limit again.
- Trigonometric identities: Limits involving trigonometric functions can often be simplified by using trigonometric identities.
- Taylor series: Taylor series can be used to approximate the value of a limit by representing the function as a polynomial.
Applications of limits:
Several scientific and engineering areas use the limits calculus. Some important applications of limits are coated below.
- Physics: In physics, limit calculus is used to study the behavior of physical systems as the input parameters approach certain values or infinity. i.e., the concept of limits is used to describe the behavior of objects moving at very high speeds or approaching the speed of light.
- Economics and finance: In economics and finance, limit calculus is used to study the behavior of economic and financial systems as certain variables approach certain values or infinity. i.e., the concept of limits is used to study the behavior of interest rates as they approach zero or infinity.
- Engineering: In engineering, limit calculus is used to study the behavior of complex systems such as mechanical systems and fluid dynamics.
- Statistics: In statistics, limit calculus is used to study the behavior of probability distributions as the number of trials or observations approaches infinity. i.e., the normal distribution’s behavior as the sample size approaches infinity is studied using the idea of limits.
Example of Limits:
In this section, we discussed examples of the limits using the techniques of the limits.
Example 1:
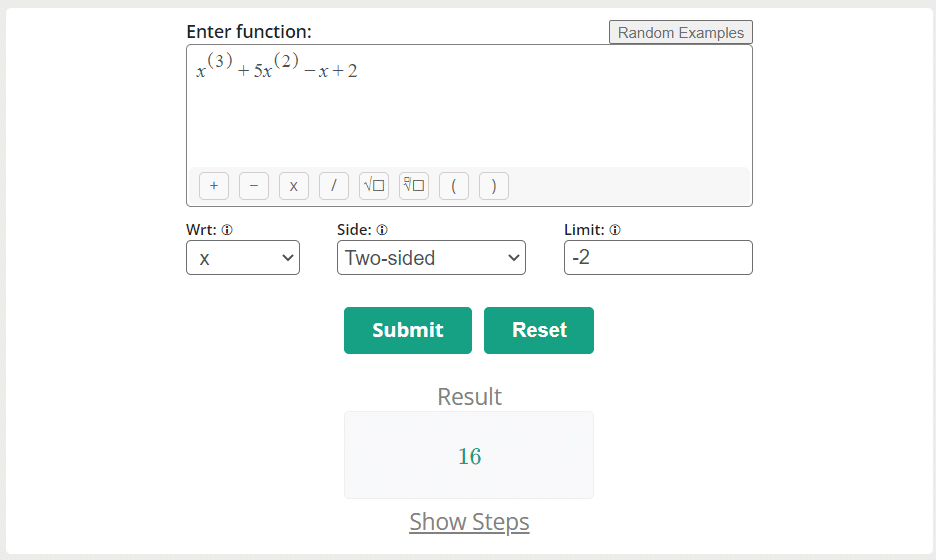
Find the limit of the x3 + 5x2 – x + 2 at “x” approaches to “-2”.
Solution:
Step 1: Let the given value is equal to F(x).
F(x) = x3 + 5x2 – x + 2
Step 2: Apply the limit on both sides and the limiting value carefully.
Lim x→-2 F(x) = Lim x→-2 (x3 + 5x2 – x + 2)
Step 3: Apply the limiting sum rule and put the limiting value carefully.
Lim x→b [F(x) – G(x) + H(x)] = Lim x→b [F(x)] – Lim x→b [G(x)] + Lim x→b [H(x)]
Lim x→-2 F(x) = Lim x→-2 (x3) + Lim x→-2 (5x2) – Lim x→-2 (x) + Lim x→-2 (2)
Lim x→-2 F(x) = (-2)3 + 5 (-2)2 – (-2) + (2)
Lim x→-2 F(x) = -8 + 5 (4) + 2 + 2
Lim x→-2 F(x) = -8 + 20 + 2 + 2
Lim x→-2 F(x) = -8 + 24
Lim x→-2 F(x) = 16
Lim x→-2 F(x) = 16 is the limit of the x3 + 5x2 – x + 2 at “x” approaches to “-2”.
Alternatively, the problems of limit calculus can be solved with the help of a limit calculator with steps to evaluate the limit of a function at a specific point without involving into lengthy calculations.
Example 2:
Find the limit of (x2-25)/(x – 5) at the limiting value of “5”.
Solution:
Step 1: Let the given value is equal to F(x).
F(x) = (x2-25)/(x – 5)
Step 2: Apply the limit on both sides and the limiting value carefully.
Lim x→5 F(x) = Lim x→5 (x2-25)/(x – 5)
Step 3: Put the limiting value in the above expression.
Lim x→5 F(x) = [(5)2-25] / [(5) – 5]
Lim x→5 F(x) = [25 – 25] / [5 – 5]
Lim x→5 F(x) = 0/0
We get a “0/0” form, for the solution of the given function apply the “Factoring and simplification” techniques.
Step 4: Factorize the term “(x2-25)” and simplify the terms.
Lim x→5 F(x) = Lim x→5 (x + 5) (x – 5)/(x – 5)
Lim x→5 F(x) = Lim x→5 (x + 5)
Step 5: Put the limiting value to get the solution.
Lim x→5 F(x) = (5 + 5)
Lim x→5 F(x) = 10
Lim x→5 F(x) = 10 is the limiting value of (x2-25)/(x – 5) as “x” approaches to “5”.
Summary:
In this article, we discussed the basic definition and epsilon-delta definition of the limits. Moreover, discussed the techniques to solve the limits and application of limits in different filed of science and engineering. To understand the concept of limits solved the examples with a detailed idea of simplification using the sum rule and techniques of limits.