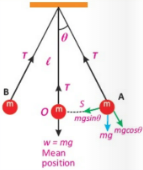A simple pendulum also exhibits SHM. It consists of a small bob of mass ‘m’ suspended from a light string of length ‘L’ fixed at its upper end.
In the equilibrium position O, the net force on the bob is zero and the bob is stationary. Now if we bring the bob to extreme position A, the net force is not zero as shown in fig.
There is no force acting along the string as the tension in the string cancels the component of the weight mg cosθ. Hence there is no motion in this direction.
The component of the weight mg sinθ is directed towards the mean position and acts as a restoring force. Due to this force the bob starts moving towards the mean position O. At O, the bob has got the maximum velocity and due to inertia, it does not stop at O rather it continues to move towards the extreme position B.
During its motion towards point B, the velocity of the bob decreases due to restoring force. The velocity of the bob becomes zero as it reaches point B. The restoring force mg sinθ still acts towards the mean position O and due to this force the bob again starts moving towards the mean position O. In this way, the bob continues it’s to and fro motion about mean position O.
It is clear from the above discussion that the speed of the bob increases while moving from point A to O due to the restoring force which acts towards O. Therefore, acceleration of the bob is also directed towards O.
Similarly, when the bob moves from O to B, its speed decreases due to restoring force which again acts towards O.Therefore, acceleration of the bob is again directed towards the mean position O.Hence the motion of a simple pendulum is SHM.
Simple pendulum Time perid formula
Consider the bob at position B during its vibratory motion as shown in the figure. Let ‘m’ be the mass of the bob and x be the displacement of the bob from the mean position at position B. There are two forces are acting on the bob at this position.
- Weight mg of the bob acting vertically downward.
- Tension T of the string acting along the direction of the string.
The weight mg of the bob can be resolved into two rectangular components:
- mg cosθ=component of weight along the string
- mg sinθ=component of the weight perpendicular to the string.
As there is no motion of the bob in the direction of the string, the component mg cosθ balances the tension in the string. So:
T = mg cosθ ……………(1)
So these two cancel each other. Therefore, the component mg sinθ is responsible for the motion of the bob which brings the bob back towards its mean position. Thus mg sinθ represents restoring force. So:
F =-mg sinθ …………….(2)
If ‘a’ is the acceleration of the bob at point B then according to Newton’s second law of motion:
F =ma ……………………(3)
Comparing equation (2) and (3), we have:
ma = -mg sinθ
⇒ a=-g sinθ ……….(4)
According to trigonometry if θ is small, the sinθ ≈θ, then equation (4) will become
⇒ a=-gθ …………..(5)
Using relation S=r θ
⇒ θ=S/r ……………………(6)
Now when θ is small ,s=arc AB =OB =x and r =l
Equation (6) now will become
⇒ θ = arc AB/l =OB/l=x/l
Now putting the value of θ in equation (5), we have
a = -g x/l …………….(7)
Since g/l is constant, therefore,
⇒ a=-(constant)x
⇒ a ∝ – x ……………..(8)
Equation (8) shows that the acceleration of the bob is directly proportional to the displacement x and the negative sign shows that it is directed towards the mean position. Hence the motion of a simple pendulum is simple harmonic.
Time period of simple pendulum
The acceleration of the body is given by:
⇒ a = -ω2x …………………..(9)
But the acceleration of simple pendulum is given by
⇒ a = -g x/l ……………………..(10)
Comparing equation (9) and (10),we have
-ω2x = -g x/l
⇒ ω2=g/l
⇒ ω =√g/l …………….(11)
The time period of a body executing SHM is given by:
T =2π/ω
Putting the value of ω from equation (11) , we have
T =2π/√g/l
⇒ T =2π √l/g ……………….(12)
Simple pendulum frequency formula
Since frequency is related to the time period as f=1/T
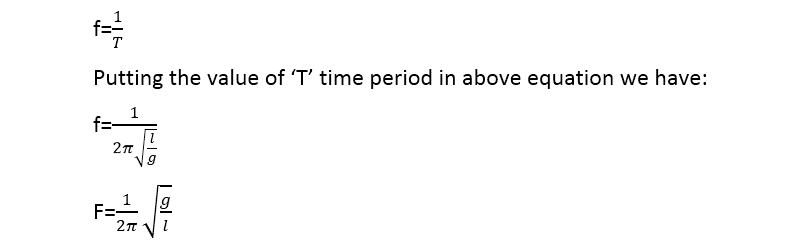
Watch also video
External sources
- https://en.wikipedia.org/wiki/Pendulum
- http://hyperphysics.phy-astr.gsu.edu/hbase/pend.html
not satisfied