Binding energy is the energy required to split the nucleus of an atom into neutrons and protons, while Mass defect is the difference b/w the predicted mass and the actual mass of the nucleus of an Atom. The binding energy of the system can appear as extra mass, which is used to find this difference.
Physically, we define the binding energy as the positive work necessary to disassemble a nucleus into its constituents (nucleons). Equivalently it is the energy liberated when Z proton and N neutrons combine to form a nucleus. For visualization, consider the simplest example of deuteron disintegration. The deuteron atom H12 has a mass of 1.014102 a.m.u while the mass of the hydrogen atom is that of the neutron
H12 = MH + MN
MH + MN = (1.007825 + 1.008665) a.m.u
= 2.016490 a.m.u
But the observed mass of the H12 is 2.014102 a.m.u which is clearly 0.002388 a.m.u greater. It is obviously evident that a mass of 0.002388 a.m.u has been reduced. when a proton and a neutron are combined to constitute the nucleus of the deuteron. A mass of 0.002388 a.m.u is equal to the Mev.
This shows that when a deuteron is formed for free proton and a neutron 2.23 Mev must be supplied from an external agency to disassemble a deuteron into a proton and a neutron. This fact is supported by an experiment in the photodisintegration of the deuteron which shows that the gamma-ray photon must have the energy of the last 2.23 Mev to disrupt a neutron.
Since the binding energy equivalent of the mass reduction of the nucleons in the nucleus is a measure of the stability of the nucleus and binding energies from the action of the forces which hold the nucleons together to form nuclei. Therefore the binding energy (B.E) of the nucleus, in general, can be written mathematically as follows:
B.E = Z MH + (A-Z) MN – M = ΔM …………..(1)
Where MH and MN are the masses of the proton and the neutron and M is the atomic mass. Thus the mass difference in the above equation obviously appears as the amount of the binding energy on forming a nucleus. The same amount of energy is required to separate the nucleons of the nucleus. It also appears that the actual mass of the nuclei is never equal to the sum of masses of its constitutions (proton + neutrons) with respect to the interior of the nucleus of the binding energy is the difference between the mutual potential energy and the total kinetic energy of the constituents nucleons i.e
B.E = P.E – K.E
The average binding energy per nucleon is obtained (from equation 1) by diving the total binding energy of the nucleus by the mass number A i.e
Average binding energy =B.E/A
Einstein’swell known energy relation E= Δmc2 shall we shall often need to use energy equivalent of 1 atomic mass unit, and we find it from
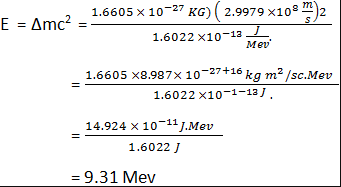
This means that we can write C2 as 931.5 Mev/u and can thus easily find energy equivalent in (Mev) of any mass or mass difference (in u) or conversely.
The main Features of Binding Energy
- A +ve binding energy for all nuclei clearly shows that any nucleus is more stable than an unconnected assembly of its constituent’s neutrons and protons.
- There is a rapid increase of binding energy per nucleon for the light nuclei with a notable peak at A = 4 (He4). This reflects the nucleon stability of the alpha-particles structure.
- Approximately the same binding energy per nucleon (7.3 Mev to 8.8 Mev) for all nuclei with A greater than 16 where A is the atomic mass.
The broad maximum in the middle represents maximum stability from about A = 56 ( Fe) to about A = 140 ( Ce).
A gradual decrease in B.E/A from maximum to 7.3 Mev /A at A = 238 (U). Evidently, the nuclei intermediate is the most stable since a greater amount of energy must be supplied to liberate each of their nucleons.
Related Topics: