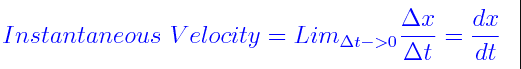Instantaneous velocity Formula
What is Instantaneous velocity?
“If a body covers small displacement in a small interval of time then its velocity will be instantaneous velocity such that Δt is equal to zero.”Where Δt is the small interval of time. Average velocity does not tell us about the motion between two points on the path. The path may be straight or curved and the motion may be steady or variable.
For example, if a squash ball comes back to its starting after bouncing off the wall several times, its total displacement is zero and so also its average velocity. In such cases, the motion is described by instantaneous velocity.
In order to understand the concept of instantaneous velocity, consider a body moving along a path as shown in the figure.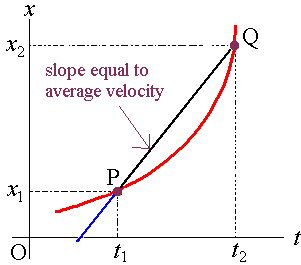
At time t 1 let the body be at point P. Its position is given X1. After a short interval time Δt following the instant t, the body reaches point Q which is described by position X2. The displacement of the body during this short time interval is given by:
ΔX = X2-X1
The instantaneous velocity at point P can be found by making Δt smaller and smaller.
Read Also: Distance Vs Displacement
In this case, ΔX will also become smaller, and point Q will approach P.If we continue this process, letting Q approach P, thus, allowing Δt and ΔX to decrease but never disappear completely, the ratio ΔX/Δt approaches a definite limiting value which is the instantaneous velocity.
Although Δt and ΔX become extremely small in this process, their ratio is not necessarily a small quantity. Moreover, while decreasing the displacement vector, ΔX approaches a limiting direction along the tangent at point P. Using the mathematical language, the definition of instantaneous velocity Vins is expressed as:
Instantaneous velocity formula