 In this post, You’ll learn how work power and energy are related to each other. This Post also includes a Work Energy and Power worksheet with answers.
In this post, You’ll learn how work power and energy are related to each other. This Post also includes a Work Energy and Power worksheet with answers.
So, If you want to get benefits from this post, then you’ll love this post.
Keep Reading…
What is work?
“Work is a task or job done when a force acts on a body and moves it in the direction of the force.”Generally, it refers to performing some task or job.
How to find work in physics?
In science, work has a precise meaning. For example, a man carrying a load is doing work but he is not doing work if he is not moving while keeping the load on his head, Scientifically, work is done only when an effort or force moves an object. When work is done, energy is used. Thus, work and energy are related to each other. The concept of energy is an important concept in physics. It helps us to identify the changes that occur when work is done.
Work done by a constant force
Consider a particle acted on by a constant force F, and assume the simplest case in which the motion takes place in a straight line in the direction of the force. In such a situation we define the work W done by the force on the particle as the product of the magnitude of the force F and the magnitude of the displacement S through which the force acts. We write this as:
Work done = Force × displacement
or W = F S
In a more general case, the constant force acting on a particle may not act in the direction in which the particle moves. In this case, we define the work done by the force on the particle as the product of the component of the force along the line of motion and the magnitude of the displacement S.
Sometimes force and displacement do not have the same direction.
Here the force F is making an angle θ with the surface on which the body is moved. Resolving F into its perpendicular components Fx and Fy as:
Fx =F cosθ
Fy =F sinθ
In case when force and displacement are not parallel then only the x-component Fx parallel to the surface causes the body to move on the surface and they-component Fy.
Hence W= Fx S
=(Fcosθ) S
=F S cosθ
Unit of work
SI unit of work is the joule (J). It is defined as:
“The amount of work is one joule when a force of one newton displaces a body through one meter in the direction of the force.”
In the British system, the unit of work is the foot-pound. In the CGS systems, the unit of work is 1 dyne centimeter, called 1 erg. Using the relations between the newton, dyne, and pound, and between the meter, centimeter, and foot, we obtain 1joule =10 7 ergs =0.7376 ft.1b. Work is a scalar, although the two quantities involved in its definition, force, and displacement, are vectors.
A convenient unit of work when dealing with atomic or subatomic particles is the electron volt (abbreviation eV ), where 1eV = 1.60 ×10-19J. The work required to remove an outer electron from an atom has a typical magnitude of several electron volts (eV). The work required to remove a proton or a neutron from a nucleus has a typical magnitude of several M eV (106eV).
Work can be either positive or negative. If a force has a component opposite to the direction of the motion, the work done by that force is negative. This corresponds to an obtuse angle between the force and displacement vectors. For example, when you lower an object by the upward force of your hand holding the object is negative. In this case, θ is 180°, for F points up and S points down. The gravitational force in this case does positive work as the object moves down.
Although the force F is invariant, independent in both the magnitude and direction of our choice of inertial frames, the displacement S is not. Depending on the inertial frame from which the measurement is made, an observer could measure essentially any magnitude and direction for the displacement Thus, observers in different inertial frames, who will agree on the forces that act on a body, will disagree in their evolution of the work done by the force acting on the body. Different observers might find the work to be positive, negative, or even zero.
Our special definition of the word “work” does not correspond to the colloquial usage of the term. This may be confusing. A person holding a heavyweight at rest in the air may be working hard in the physiological sense, but from the point of view of physics, that person is not doing any work on the weight. We say this because the applied force causes not the displacement of the weight.
If, on the other hand,w consider the weightlifter to be a system of particles, we find that microscopically work is indeed being done a muscle is not solid support and cannot sustain a load in a static manner. The individual muscle fibers repeatedly relax and contract, and if we analyze the situation in this manner we would find that work is done in each contraction. That is why the weightlifter becomes tired of supporting the weight.
If there are a number of forces acting on the body, then the work done is separately calculated for each force. Then the network will be the sum of work done by all separate forces.
Case 1:
If the displacement is produced in the direction of the force i.e,θ = 0°, then the work done will be:
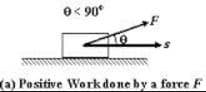
W = FS cos0°
we know that cos 0°=1
So:
W = F S (1)
W=FS
Thus, when a horizontal force moves a body horizontally or when a vertical force lifts a body vertically, then the work done is the product of force and distance covered by the object.
Case 2(If θ = 90°):
When the force has no component in the direction of motion, then no work is done by the force.
W =FS cos(90°)
W=FS cos(0)
W=0
Thus, if a person carrying a weight walks horizontally, then the force exerted by the man is perpendicular to the horizontal displacement. So, no work is done. The examples of forces which don’t work are:
- Centripetal force
- Tension in the string of vibrating pendulum
- Weight and normal force don’t work because they are perpendicular to the displacement
Case 3(if θ =180°):
When the force has a component opposite to the direction of displacement, then the work done by the force is: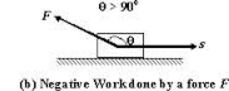
W =FS cos(180°)
W =FS (-1)
W=-FS
The force of friction is opposite to the direction of motion, so the work done by the force of friction on the object is zero.
What is energy?
“Energy is the ability of a body to do work.”
The quantity is the measure of the capacity of a body or a system for doing work. When a body does work, W, its energy decreases by an amount equal to W. The energy of a body upon which it does work increases by exactly the same amount so that the total energy of the system does not change. This is the principle of conservation of energy.
The interaction of two bodies causes the transfer of energy between them. The kind of energy may be unchanged, or it may be partially or wholly changed. If two bodies are at different temperatures, it is possible for energy, Q, to be transferred from that at high temperatures to that at lower without any apparent forces and displacements by which work could be done. This is the process of heat, which involves work on the molecular scale.
Energy makes change possible. We use it while doing things. It moves cars along the road and boats over the water. It cooks our food and keeps ice frozen in the freezer. It plays our favorite songs on the radio and lights our homes. It also needed our body to grow.
In an avalanche, a mass of loose snow, soil, or rock suddenly gives away and slides down the side of a mountain. The avalanche releases a great amount of energy.
The unit of energy is the joule. It is represented by J. The unit of energy is the same as that of work. One joule is defined as the amount of work done when a body covers a distance of one meter in the direction of one Newton force.
1 J =1 Nm
In the study of energy, we would like you to keep five important aspects of this concept in mind:
- Energy brings about changes in the world.
- Energy can be transferred from one place to another.
- Energy can be converted from one form to another.
- In energy conversations and transfers, the total amount does not change.
- Some forms of energy are more useful than others.
What is Power?
The definition of work makes no reference to the passage of time. If you lift a barbell weighing 100 N through a vertical distance of 1.0 m at a constant velocity, you do (100 N)(1 m)=100 J of work whether it takes you 1 second,1 hour, or 1 year to do it. But often we need to know how quickly work is done. We describe this in terms of power. In ordinary conversation, the word “power” is often synonymous with “energy” or “force”.In physics, we use a much more precise definition. Power is the time rate at which work is done. Like work and energy, power is a scalar quantity.
Unit of power
Since work is a scalar quantity, therefore, power is also a scalar quantity.SI unit of power is the watt (W). It is defined as: “The power of a body is one watt if it does work at the rate of 1 joule per second (1 J s-1).”Sometimes, for example, in the electrical measurements, the unit of work is expressed as watt-second. However, a commercial unit of electrical energy is kilowatt-hour. One kilowatt-hour is the work done in one hour by an agency whose power is one kilowatt.
Work energy and power problems and solutions
- A machine does 20 joules of work in 4 seconds. Find its power.
Solution:
Given data: time=t= 4s
Work =W = 20J
Power =P=?
Formula= P =W/t
P=20J/4s
P=5 W
- A man has pulled a cart through 35m by applying a force of 300 N.Find the work done by the man.
Solution:
Given data: Distance =S =35 m
Force =F=300 N
Work = ?
Formula: Work = Force × distance
W= F × S
W = 35 × 300
W=10500 J
Work power and Energy worksheet (video)
Related Topics:
One Comment