Different Types of motion in Physics with Examples

Basically, there are three types of Motion, Translatory motion, Rotatory motion, and Vibratory motion. Some Other Examples of Motion are Linear motion, Random motion, Circular motion, Uniform, and Non-Uniform Motion.
This post also includes lots of:

Motion definition
Real-life motion examples
Images
Types
Video
Lots more

So if you want to learn Motion and Type of Motion, You’ll love this post.
Let’s dive right in.

What is motion in Physics?

Surroundings are the places in their neighborhood where various objects are present. The state of rest or motion of a body is relative.
For example, a passenger sitting on a moving bus is at rest because he is not changing his position with respect to other passengers or objects on the bus. But to an observer outside the bus, the passengers and the objects inside the bus are in motion.
Therefore we can define rest as “A body is said to be at rest if it does not change its position with respect to its surroundings.
We live in a universe of continual motion. In every piece of matter, the atoms are in a state of never-ending motion. We move around the Earth’s surface, while the earth moves in its orbit around the sun. The sun and the stars, too, are in motion.
Everything in the vastness of space is in a state of perpetual motion. Every physical process involves the movement of some sort. Because of its importance in the physical world around us. It is logical that we should give due attention to the study of motion. Motion is commonly described in terms of:

Displacement
Distance
Time
Speed

How many types of motion in physics?

If we observe carefully, we will find that everything in the universe is in motion. However, different objects move differently.
Some objects move along a straight line, some move in a curved path, and some move in some other way. According to this, we can say that there are three types of motion. Which are given as:

- Translatory motion
- Rotatory motion
- Vibratory motion

What is Translatory motion?

“In translational motion, a body moves along a line without any rotation. The line may be straight or curved.”Watch how various objects are moving. Do they move along a straight line? Do they move along a circle? A car moving in a straight line has transnational motion. Similarly, an airplane moving straight is in translational motion. Translatory motion is further divided into linear motion, circular motion, and random motion.

Tranaslatory motion Examples

- - Motion of train
  - motion of earth
  - motion of birds
  - motion of insects
  - motion of airplane
  - the motion of gas molecules

Learn more about: Difference between uniform and non-uniform motion

What is Linear motion?

“Straight-line motion of a body is known as its linear motion.”

We come across many objects which are moving in a straight line. The motion of objects such as cars moving on a straight and level road is linear motion. Airplanes flying straight in the air and objects falling vertically down are also examples of linear motion.
In the above diagram, a boy is sliding in a straight line which is an example of linear motion.

Linear motion examples in daily life

- - The motion of the car on the road
  - Motion of football
  - Sliding a boy in a straight line is an example of linear motion

Circular motion

“The motion of an object in a circular path is known as circular motion.”A toy train moving on a circular track. Earth revolving around the sun is an example of circular motion.

A bicycle or a car moving along a circular track possesses circular motion. The motion of the moon around the earth is also an example of circular motion.

Examples of circular motion in daily life

- - The motion of the electron around the nucleus
  - The motion of the toy car on the circular track
  - The motion of planets around the sun

Random motion

“The disordered or irregular motion of a body is called random motion.”Have you noticed the type of motion of insects and birds? Their movements are irregular and disorderly. The motion of insects and birds is a random motion example. The motion of dust or smoke particles in the air is also a random motion. The Brownian motion of a gas or liquid molecules along a zig-zag is also an example of random motion.”The random motion of gas molecules is called Brownian motion.”
This may help you: Equations of motion

What is Rotatory motion?

“The spinning motion of a body about its axis is called its rotatory motion.”
Study the motion of a tap. It is spinning about an axis. Particles of the spinning top move in circles and thus individual particles possess circular motion. Does the top possess circular motion?
The top spins about its axis passing through it and thus it possesses rotatory motion. An axis is a line around which a body rotates. In a circular motion, the point about which a body goes around is outside the body. In rotatory motion, the lone, around which a body moves about, is passing through the body itself.
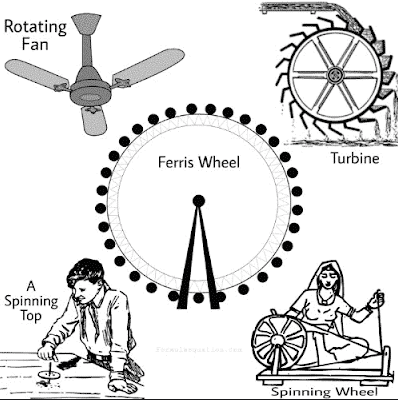
rotational motion

Rotatory motion examples

- - The motion of the earth about its geographic axis that causes day and night is rotatory motion.
  - The motion of the wheel about its axis and that of the steering wheel are examples of rotatory motion.

What is Vibratory motion?

“The motion of a body about its mean position is known as vibratory motion.”

Consider a baby in a swing as shown in the above figure. As it is pushed, the swing moves back and forth about its mean position. The motion of the baby repeats from one extreme to the other extreme with the swing.
The motion of the pendulum of a clock about its mean position is also an example of vibratory motion.
Children playing in a sea-saw is an example of vibratory motion.
Besides these examples a baby in a cradle moving to and fro, to and fro motion of the hammer of a ringing electric bell and the motion of the string of a sitar are some of the examples of vibratory motion. Simple harmonic motion is also an example of vibratory motion.