What is Schrodinger wave equation?
Schrodinger wave equation describes the wave function or state function, There are two types of Schrodinger equations, time-dependent Schrodinger wave equation, and time-independent Schrodinger wave equation. These equations were presented by Ervin Schrodinger in 1925.
In classical mechanics, the motion of a body is given by Newton’s second law of motion. But elementary particles like electron, protons, and photons possess wave properties as well, therefore another equation instead of Newton’s second law equation ( F=ma) is required for describing their motion.
The new equation must take into account wave properties of particles and it should, therefore, be similar to the equation describing wave on strings acoustic waves or electromagnetic waves. This equation was found in 1926 by the Austrian physicist Schrodinger and is known after his name as Schrodinger wave equation.
Schrodinger wave equation derivation
Consider a particle of mass “m” moving with velocity “v” in space. Suppose a system of stationary waves is associated with the particles at any point in space in the neighborhood of particles.
We know that:

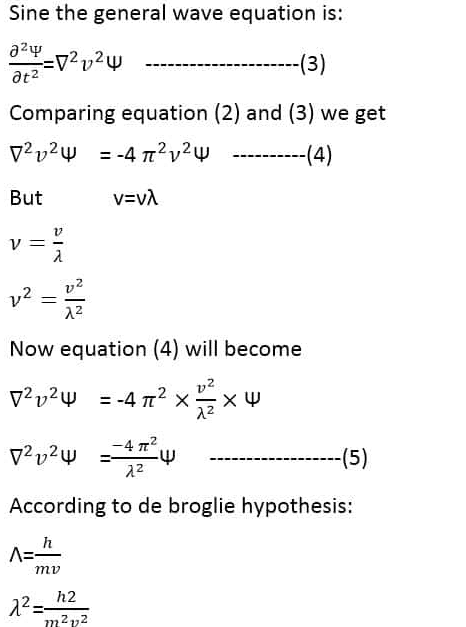
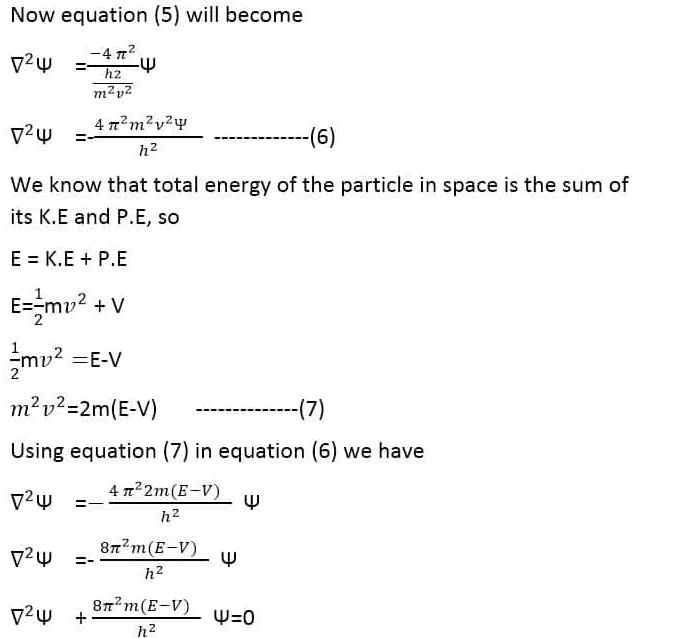
This is the Schrodinger time-independent wave equation.
See also: Schrodinger time-dependent wave equation