Schrodinger time-dependent wave equation is a partial linear differential equation that describes the state function or wave function of a quantum mechanics system. It is a very important result in quantum mechanics or modern physics. This equation was presented by Ervin Schrodinger in 1925 and published in 1926.
Schrodinger time-dependent wave equation derivation
Consider a particle of mass “m” with velocity “v” and under the influence of potential energy (P.E) which is represented by V(r) . The total energy of the particle is the sum of potential energy (P.E) and kinetic energy (K.E) which is given by:
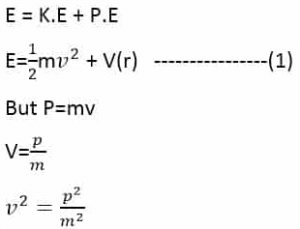
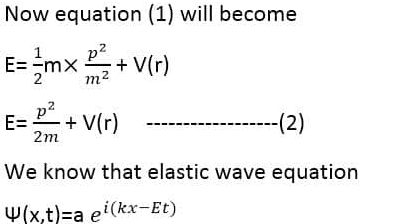
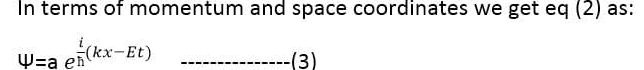
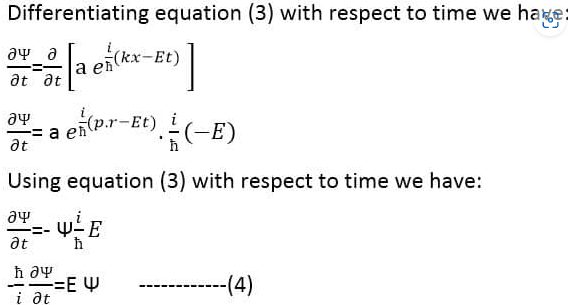
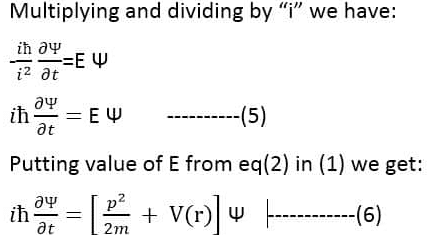
This is the Schrodinger time-dependent wave equation formula.
The factor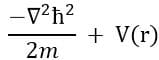 
=H is known as a Hamiltonian operator which gives the energy of the particle. Now equation (7) can be written as:
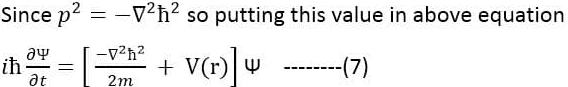
See also: Schrodinger time-independent wave equation