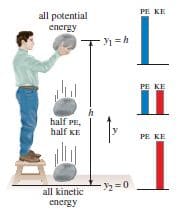
Conservation of mechanical energy is defined as “the total mechanical energy of a system neither increases nor decreases in any process”. A simple example of the conservation of mechanical energy is a rock allowed to fall due to Earth’s gravity from a height h above the ground.
Examples of conservation of mechanical energy
A roller-coaster car moving without friction illustrates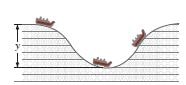
the conservation of mechanical
energy.
Conservation of Mechanical Energy formula
To see what gravitational potential energy is good for, suppose the body’s weight is the only force acting on it, so:
The body is then falling freely with no air resistance and can be moving either up or down. Let is speed at point y1 be v1 and let its speed at y2 be v2. The work energy-theorem, say that the total work done on the body equals the change in the body’s kinetic energy:
Wgrav = ∆K = K2 – K1 .
If gravity is the only force that acts,then from equation,
Wnot = Wgrav = -∆Ugrav = Ugrav,1 – Ugrav,2.
Putting these together, we get:
∆K = -∆Ugrav or K2 – K1 = Ugrav,1 – Ugrav,2
which we write as:
K1 + Ugrav,1 = K2 + Ugrav,2 ……….eq (1)
Or
mv + mgy1 ………….eq (2)
The sum K+ Ugrav of kinetic and potential energy is called E, the total mechanical of the system. By “system” we mean the body of mass m and the earth considered together because gravitational potential energy U is a shared property of both bodies.
Then E1 = K1 + Ugrav,1 is the total mechanical energy at y1, and E2 = K2 + Ugrav,2 is the total mechanical energy at y2 . Equation (1) says that when the body’s weight is the only force doing work on it E1 = E2 . That is, E is constant; it has the same value at y1 and y2 . but since the positions y1 and y2 are arbitrary points in the motion of the body, the total mechanical energy E has the same value at all points during the motion:
E = K + Ugrav = constant
A quantity that always has the same value is called a conserved quantity. When only the force of gravity does work, the total mechanical energy is constant-that is, is conserved. This is our first example of the conservation of mechanical energy.
When a throw a ball into the air, its speed decreases on the way up as kinetic energy is converted to potential energy; ∆K < 0 and ∆ Ugrav >0. On the way back down, potential energy is converted back to kinetic energy, and the ball’s speed increases; ∆K > 0 and ∆ Ugrav < 0.
But the total mechanical energy (kinetic plus potential) is the same at every point in the motion, provided that no force other than gravity does work on the ball (that is, air resistance must). While this athlete is in midair, only gravity does work on him(if we neglect the minor effect of air resistance). Mechanical energy E-the sum of kinetic and gravitational potential energy is conserved.
It’s still true that the gravitational force does work on the body as it moves up or down, but we no longer have to calculate work directly; keeping track of changes in the value of Ugrav takes care of this completely.
Let see video now :
Related topics