Dimensional analysis Examples

Dimensional analysis definition

All the physical quantities can be expressed in terms of seven fundamental quantities. The powers to which these fundamental physical quantities be raised are termed as “dimensions”. Using the method of dimensions called dimensional analysis.

Each base quantity is considered a dimension expressed by specific symbol written within square brackets. It stands for qualitative nature of physical quantity. For example different quantities such as length ,width, diameter, light year are measured in meter denote the same dimension and has dimension of length [L ].

Similarly mass and time dimensions are denoted by [M] and [T] respectively. Other quantities that we measure have dimension which are combinations of these dimensions. For example speed is measured in meters per second. This will obviously have the dimensions of length divided by time.

Some Dimensional Analysis Examples

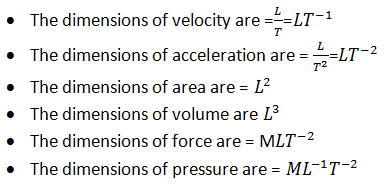
Applications of dimensional analysis in physics

• To check the correctness of given physical relation, it is based on the principle of homogeneity, that is the dimensions on two sides for a given relation. For example if L.H.S and R.H.S have identical dimensions, therefore the relations are dimensionally correct. If the dimensions on two sides differ, the relation is incorrect.
• It is used to convert the value of physical quantity from one system of units to another system of units.
• It is used to denote the nature of physical quantity.
• Dimensional analysis makes use of the fact that expressions of the dimensions can be manipulated as algebraic quantities.
• It is used to derive the possible formula.

You may search Also:

• Types of physical quantities
• Difference between scientific notation and significant figures
• Difference between accuracy and precision
• Types of errors in physics
• Vernier caliper least count formula
• Screw Gauge least count formula