Examples of Simple Harmonic Motion

Simple harmonic motion is the kind of vibratory motion in Physics in which the body moves back and forth about its mean position. Examples of simple harmonic motion are: – A sheet fixed at one end and vibrating at the other end. – A system formed by a body suspended from a spring. – The motion of a pendulum for small displacements. – A liquid contained in a U-bent tube.

This post Includes:

• Introduction of SHM
• Examples Of S.H.M in real life
• Conditions
• Equation
• Lot’s more

Keep Reading..

Simple harmonic motion examples

• The motion of a mass attached to spring
• Ball and Bowl system
• The motion of simple pendulum
• Atoms vibrating in molecules
• The vibration of the string of a violin

Conditions of SHM

• The acceleration of the oscillator should be directly proportional to its displacement and always be directed towards the mean position.
• Total energy must remain conserved.
• There must be an elastic restoring force acting on the system.
• The restoring force must be directly proportional to the displacement from the mean position. (The system must obey Hook’s law).
• The oscillator in SHM must have inertia.

Simple harmonic Oscillator equation

“A body executing simple harmonic motion is called a simple harmonic oscillator.” OR “A vibrating body is said to be a simple harmonic oscillator if the magnitude of restoring force is directly proportional to the magnitude of its displacement from the mean position. The vibration of the simple harmonic oscillator will be linear when frictional forces are absent.’ Examples:

• The motion of a mass attached to spring
• The motion of simple pendulum
• Atoms vibrating in molecules

We will discuss a few examples in detail:

•  Motion of mass attached to a spring

One of the simplest types of oscillatory motion is that of a horizontal mass-spring system. If the spring stretched or compressed through a small displacement x from its mean position, it exerts a force F on the mass. According to Hooke’s law, this force is directly proportional to the change in length x of the spring i.e.,

                                       F =-Kx ………….(1)

Where x is the displacement of the mass from its mean position O, and k is a constant called spring constant defined as:

                                       k=-F/x

The value of k is a measure of the stiffness of the spring. Stiff springs have a large value of k and soft springs have a small value of k. As we know:

                             F=ma

Therefore:

                               a=F/m

or

                               a=-kx/m

If (k/m) is constant then:

                                 a ∝ -x   …………..(2)

It means that the acceleration of a mass attached to a spring is directly proportional to its displacement from the mean position. Hence, the horizontal motion of a mass-spring system is an example of simple harmonic motion. The negative sign in equation (2) means that the force exerted by the spring is always directed opposite to the displacement of the mass. Because the spring force always acts towards the mean position, it is sometimes called a restoring force. Which is defined as: “A restoring force always pushes or pulls the object performing oscillatory motion towards the mean position.”

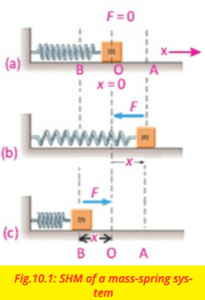Initially, the mass m is at rest in mean position O and the resultant force on the mass is zero as shown in figure(a). Suppose the mass is pulled through a distance x up to extreme position A and then released as shown in figure (b). The restoring force exerted by the spring on the mass will pull it towards the mean position O.Due to the restoring force magnitude of the restoring force decreases with the distance from the mean position and becomes zero at O.However, the mass gains speed as it moves towards the mean position and its speed becomes maximum at O. Due to inertia the mass does not stop at the mean position O but continues its motion and reaches the extreme position B. As the mass moves from the mean position O to the extreme position B, the restoring force acting on it towards the mean position steadily increases in strength. Hence the speed of the mass decreases as it moves towards extreme position B. The mass finally comes briefly to rest at the extreme position B as shown in figure (c). Ultimately the mass returns to the mean position due to the restoring force. This process is repeated, and the mass continues to oscillate back and forth about the mean position O.Such motion of a mass attached to a spring on a horizontal frictionless surface is known as simple harmonic motion (SHM). The time period T of the simple harmonic motion of a mass attached to a spring is given by the following equation:

 

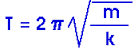
How is energy conserved in SHM?

Let us consider the case of a vibrating mass-spring system. When the mass m is pulled slowly, the spring is stretched by an amount x₀ against the elastic restoring force F.It is assumed that stretching is done slowly so that acceleration is zero. According to Hook’s law
F=Kx₀
When                     displacement =0                 force=0
When                      displacement=x₀               force=kx₀
The average force is:

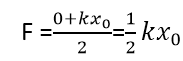
Work done in displacing the mass m through x₀ is:

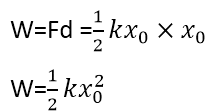
This work appears as the elastic potential energy of the spring. Hence

The above equation gives the maximum P.E. at the extreme position. Thus

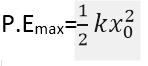
At any instant t, if the displacement is x, then P.E at that instant is given by:

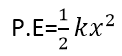
The velocity at that instant is given by the equation:

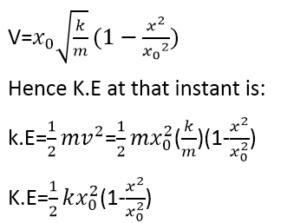
Thus kinetic energy is maximum when x=0,i.e .when the mass is at equilibrium or mean position:

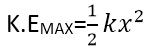
For any displacement x, the energy is partly P.E and partly K.E.Hence:

Thus the total energy of the vibrating mass and spring is constant. When the K.E of the mass is maximum, the P.E of the spring is zero. Conversely, when the P.E of the spring is maximum, the K.E of the mass is zero. The interchange occurs continuously from one form to the other as the spring is compressed and released alternately. The variation of P.E and K.E with displacement is essential for maintaining oscillations. This periodic exchange of energy is a basic property of all oscillatory systems. In the case of a simple pendulum gravitational P.E of the mass, when displaced, is converted into K.E at the equilibrium position. The K.E. is converted into P.E. as the mass raises to the top of the swing. Because of the frictional forces, energy is dissipated and consequently, the systems do not oscillate indefinitely.

Watch also video about simple harmonic motion:  
Related Topics:

• Simple Pendulum
• Types of motion
• Types of Waves
• Mechanics