The speed of sound can be calculated by the formula:
Speed of sound = Frequency of sound wave * Wavelength
v = f ×λ
Sound waves can be transmitted by any medium containing particles that can vibrate. They cannot pass through the vacuum. However, the nature of the medium will affect the speed of the sound waves. In general, the speed of sound in a liquid is five times that in gases; the speed of sound in a solid is about fifteen times that in gases. The speed of sound in air is affected by changes in some physical conditions such as temperature, pressure, humidity, etc.
Sound waves are the most important examples of longitudinal or compressional waves. The speed of sound waves depends on the compressibility and inertia of the medium through which they are traveling. If the medium has the elastic modulus E and density ρ then, speed v is given by:
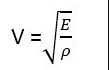
The table has given of speed of sound in different media at 25 c°.
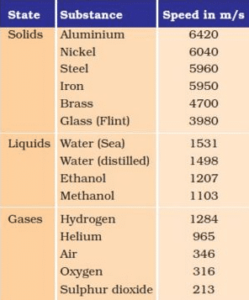
As seen from the table, the speed of sound is much higher in solids than in gases. This makes sense because the molecules in a solid are closer than in gas and hence, respond more quickly to a disturbance.
In general, sound travels more slowly in gases than in solids because gases are more compressible and hence have a smaller elastic modulus. For the calculation of elastic modulus for air, Newton assumed that when a sound wave travels through air, the temperature of the air during compression remains constant and pressure changes from p to (p + Δp), and therefore, the volume changes from V to (V – ΔV).
According to Boyle’s law:
PV =(P + ΔP )(V – ΔV ) …..(1)
OR
PV =PV -PΔV +VΔP – ΔPΔV
The product of ΔPΔV is very small and can be neglected. So, the above equation becomes:
PΔV = VΔP or
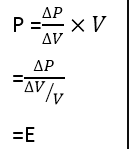
The expression (ΔP/ΔV/V) is the elastic modulus E at a constant temperature. So, substitute P for E in relation given below:
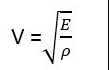
we get Newton’s formula for the speed of sound in air. Hence
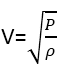
On substituting the values of atmospheric pressure and density of air at S.T.P in equation ….relation, we find that the speed of sound waves in the air comes out to be 280 ms-1, whereas its experimental value is 332 ms-1.
To account for this difference, Laplace pointed out that the compression and rarefactions occur so rapidly that heat of compression remains confined to the region where it is generated and does not have time to flow to the neighboring cooler regions which have undergone an expansion. Hence the temperature of the medium does not remain constant. In such cases, Boyle’s law takes the form
PVϒ=Constant
Where γ=Molar specific heat of the gas at constant pressure/Molar specific heat of the gas at constant volume
If the pressure of a given mass of a gas is changed from P to (P +ΔP) and volume changes from V to (V -ΔV), then using relation PVϒ=Constant we get:
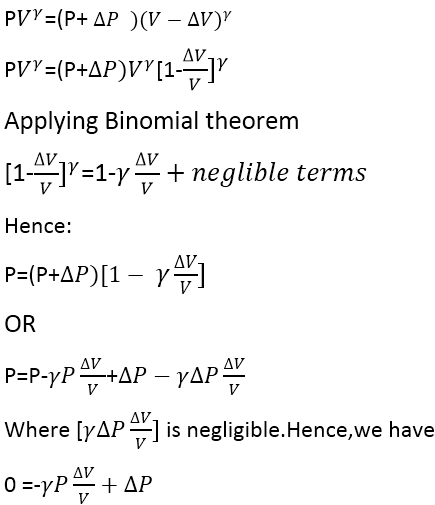
Speed of sound (video)
Related posts: