Square Properties With Examples

A square is a two-dimensional plane shape having four equal sides and all four angles equal to 90 degrees, according to geometry. The features of a rectangle are similar to those of a square, however, the difference is that a rectangle only has equal opposite sides. As a result, a rectangle is only considered a square if all four sides are the same length.

Definition of Square

The square is a polygon with four equal sides ( quadrilateral ). Its four interior angles are also equal and straight (90º each).

Parts of Square

• Sides: the square has four sides ( a ) equal and parallels two to two.
• Angles: it has four equal and right angles (α) of 90º (π/2 radians). The interior angles, as in all quadrilaterals, add up to 360º (2π radians).
• Diagonals – Diagonals are segments joining opposite vertices. It has two equal and perpendicular diagonals ( D ₁ and D _{2 ).} They intersect in the center of the square. The diagonals are the bisectors of the angles. They are also lines of symmetry.
• Symmetry axes are imaginary lines that divide the square into two symmetrical parts with respect to said axis. It has four axes of symmetry ( E ₁, E ₂, E _3, and E ₄ ).

The square is a particular case of the rectangle, the pairs of sides being equal. It is also a particular case of the rhombus, with pairs of equal and right angles (90º).

Square Shape

A square is a four-sided polygon with all four sides equal in length and all angles measuring 90 degrees. The square’s shape is such that if a plane is sliced through it from the center, both parts are symmetrical. Each half of the square now resembles a rectangle with equal sides on both sides.

Square Properties

The following are the most important properties of a square:

• Each of the four inside angles is 90 degrees.
• The square’s four sides are congruent or equivalent to one another.
• The square’s opposite sides are parallel to each other.
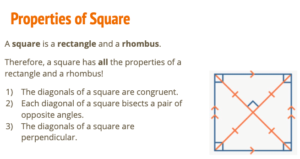
• The square’s diagonals are 90 degrees apart and bisect each other.
• The square’s two diagonals are equal in length.
• The square has four sides and four vertices.
• The square’s diagonal divides it into two identical isosceles triangles.
• The length of the diagonals exceeds the length of the square’s sides.

How to find Area and Perimeter of Square?

The area and perimeter are the two fundamental characteristics that distinguish a square from other shapes. Let’s have a look at them one by one:

Area of Square

The area of the square is the region enclosed by it in a two-dimensional plane. The area of the square here is equal to the square of the sides. It is measured in square units.

           Area = side² per square unit

If ‘x’ is the length of the side of the square, then;

Area = x² sq.unit

Perimeter of Square

The square’s perimeter is equal to the sum of its four sides. The perimeter is measured in the same unit as the square’s side length.

Perimeter = Side + Side + Side + Side = 4 Side

Perimeter = 4 × side of the square

If ‘x’ is the length of the side of the square, then the perimeter is:

Perimeter = 4x unit