Bernoulli equation derivation with examples and applications

Bernoulli equation is defined as the sum of pressure, the kinetic energy and potential energy per unit volume in a steady flow of an incompressible and nonviscous fluid remains constant at every point of its path.”Atomizer and ping pong ball in Jet of air are examples of Bernoulli’s theorem, and the Baseball curve, blood flow are few applications of Bernoulli’s principle.

Bernoulli’s principle formula

P+ ρgh +1/2 ρv² =constant

Bernoulli’s equation, which is a fundamental relation in fluid mechanics, is not a new principle but is derivable from the basic laws of Newtonian mechanics. We find it convenient to derive it from the work-energy theorem, for it is essentially a statement of the work-energy theorem for fluid flow.

Bernoulli equation derivation

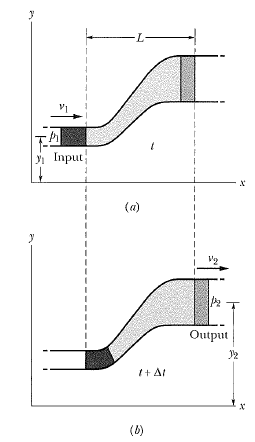
Consider the steady, incompressible, nonviscous, and irrotational flow of a fluid through the pipeline or tube of the flow as shown in the figure. The portion of the pipe shown in the figure has a uniform cross-section A₁, at the left. It is horizontal there at an elevation y₁ above some reference level. It gradually widens and rises and at the right has a uniform cross-section A₂. It is horizontal there at an elevation y₂. At all points in the narrow apart of the pipe the pressure is p₁ and the speed v₁; at all points in the wide portion the pressure is p₂ and the speed is v₂.

The work-energy theorem states: The work done by the resultant force acting on a system is equal to the change in kinetic energy of the system. In the figure, the forces that do work on the system, assuming that we can neglect viscous forces, are the pressure forces p₁A₁ and p₂A₂ that act on the left and right-hand ends of the system, respectively, and the force of gravity. As fluid flows through the pipe the net effect. We can find the work W done on the system by the resultant force as follows:

1. The work is done on the system by the pressure force p₁A₁ and p₁A₁Δl₁.
2. The work done on the system by the pressure force p₂A₂ is p₂A₂Δl₂ . Note that it is negative because the force acts in a direction opposite to the horizontal displacement.
3. The work done on the system by gravity is associated with lifting the fluid element from height y₁ to height y₂ and is -Δmg(y₂ – y₁) in which Δm is the mass of fluid in either area. This contribution is also negative because the gravitational force acts in a direction opposite to the vertical displacement.

The network W done on the system by all the forces is found by adding these three terms, or

W = p₁A₁Δl₁ – p₂A₂Δl₂ -Δmg(y₂ – y₁)

Now A₁Δl₁ and A₂Δl₂ is the volume of the fluid element which we can write as Δm _{/ρ ,} in which ρ  is the constant fluid density. Recall that the two-fluid elements have the same mass, so in a setting:

A₁Δl₁ = A₂Δl₂

we have assumed the fluid to be incompressible. With this assumption we have

W=(p₁ –p₂)(Δm_/ρ – Δmg(y₂-y₂) ………….(1)

The change in kinetic energy of the fluid element is:

From the work-energy theorem, W=Δk,we then have:

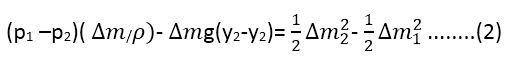
After canceling the common factor of m, we can be rearranged to read:

Since the subscript 1 and 2 refer to any two locations along the pipeline, we can drop the subscript and write:

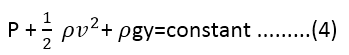
Equation (4) is called Bernoulli’s equation for steady, incompressible, nonviscous, and irrotational flow. It was first presented by Daniel Bernoulli in his Hydrodynamica in 1738.

Applications of Bernoulli’s principle

• venturi tube
• Baseball Curve
• Sailboats
• Torricelli’s theorem
• Blood Flow

Watch video also:

Related topics:

• Continuity equation
• Viscosity
• Terminal velocity