Heisenberg uncertainty principle

Heisenberg uncertainty principle Equation is provided here. If you want to get benefits from this post, you’ll love this post.
This post includes:
Heisenberg uncertainty principle:

• Definition
• Formula
• Equation
• Significance
• lot’s more

Keep reading

 Heisenberg  uncertainty principle Statement

The uncertainty principle is defined as: “It is impossible to measure simultaneously both the position and momentum of a microscopic particle with accuracy or certainty.”

When we are studying a large moving object say a planet, then we can follow its definition path on which it travels. If we know its initial position and momentum, then we can predict its position and momentum at any other time. But this is not possible for electrons, protons, and neutrons which are microscopic particles. Heisenberg has given a principle in this connection.

 Uncertainty principle proof

In order to know the position of an object, we throw the photons of light upon them. If we want to have the idea for the position of the electron, then the photons of X -rays region have to be used because their wavelengths are very small and the possibility for the hitting of the electron is there. During this hitting, the photon transfers some of its energy to the electron. Therefore, the velocity and hence the momentum of the electron changes.

If we use the photons of longer wavelengths say of visible region, the velocity and the momentum will not change appreciably because longer wavelengths rarely find the chance to hit the electron. However, its position cannot be determined because the object will not be visible.

Keep in mind that, the uncertainty is not due to a lack of better techniques for the measurement of position and momentum. This is due to the reason that we cannot observe the microscopic objects without disturbing them. The uncertainty principle is not applicable to stationary electrons because, in the stationary state, the velocity of an electron is zero. As a result, the position of the electron can be accurately determined. However, both positions and velocities of an electron cannot be determined accurately.

Heisenberg uncertainty principle Equation

Let the motion of the particle is along the x-axis, then according to the de Broglie Hypothesis:

If the motion of the particle depends upon the three coordinates x,y,z the generalizing above relation, we have:

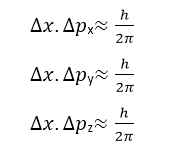
These are known as Heisenberg’s uncertainty relationships. According to these relationships: It is impossible to determine both the position and the momentum of a particle with ultimate precision.

The width Δx of the wave packet indicates the problem location of the particle, and Δp_x is the range in momentum. So, the uncertainty principle may also be stated as:

“A particle cannot be described by a wave packet in which the position and momentum have arbitrary small ranges.”

It means that due to the wave nature, the exact position x of a particle cannot be determined, but it will be in the range Δx. Similarly, the true or exact momentum of the particle p_x cannot be determined, but it will be in the range of Δp_x.

Watch also:

Related Topics:

• • Postulates of Bohr’s model of an atom
  • Dual nature of matter
• Schrodinger wave equation
  • Schrodinger time-dependent wave equation
  • Schrodinger time-independent wave equation
• Laser
  • What is a laser? How does it work?
  • What are the different types of lasers?
  • Uses of laser in daily life
  • Helium (he) Neon (ne) laser working animation
  • Properties and applications of laser light