Maxwell’s Equations: Derivation in Integral and Differential form

Maxwell’s equations are the basic equations of electromagnetism which are a collection of Gauss’s law for electricity, Gauss’s law for magnetism, Faraday’s law of electromagnetic induction, and Ampere’s law for currents in conductors. Maxwell equations give a mathematical model for electric, optical, and radio technologies, like power generation, electric motors, wireless communication, radar, and, Lenses, etc.
These Equations explain how magnetic and electric fields are produced from charges.
These equations are part of the comprehensive and symmetrical theory of electromagnetism, which is essential to understand electromagnetic waves, optics, radio and TV transmission, microwave ovens, and magnetically levitated trains.
What are the four of Maxwell’s Equations?
The four of Maxwell’s equations for free space are:
The First Maxwell’s equation (Gauss’s law for electricity)
Gauss’s law states that flux passing through any closed surface is equal to 1/ε0 times the total charge enclosed by that surface.
The integral form of Maxwell’s 1st equation
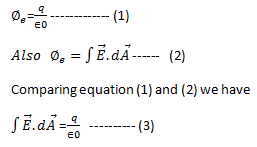
It is the integral form of Maxwell’s 1st equation.
Maxwell’s first equation in differential form
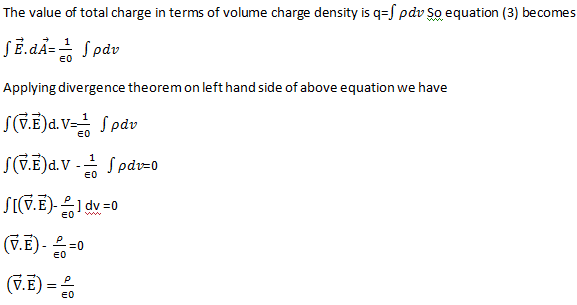
It is called the differential form of Maxwell’s 1st equation.
The Second Maxwell’s equation (Gauss’s law for magnetism)
Gauss’s law for magnetism states that the net flux of the magnetic field through a closed surface is zero because monopoles of a magnet do not exist.
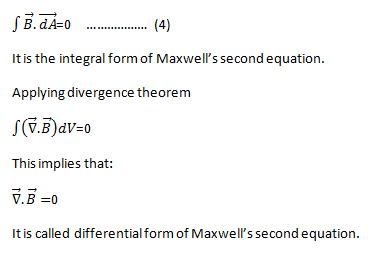
The Third Maxwell’s equation (Faraday’s law of electromagnetic induction )
According to Faraday’s law of electromagnetic induction

It is the differential form of Maxwell’s third equation.
Visit Our Page for Related Topics: Electromagnetism
Suggested Video:
The Fourth Maxwell’s equation ( Ampere’s law)
The magnitude of the magnetic field at any point is directly proportional to the strength of the current and inversely proportional to the distance of the point from the straight conductors is called Ampere’s law.
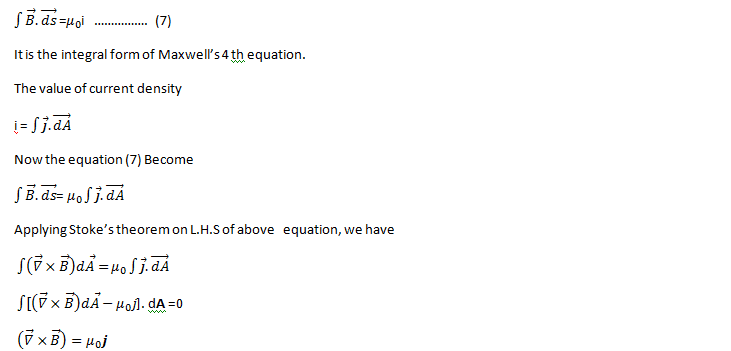
Third Maxwell’s equation says that a changing magnetic field produces an electric field. But there is no clue in the fourth Maxwell’s equation whether a changing electric field produces a magnetic field? To overcome this deficiency, Maxwell’s argued that if a changing magnetic flux can produce an electric field then by symmetry there must exist a relation in which a changing electric field must produce a changing magnetic flux.
For more related informative topics Visit our Page: Electricity and Magnetism
Related Topics:
Physics Related Links:
Handpicked links
The full proof of fourth equation of Maxwell is missing…
We must consider the the solar corona free electrons im which our Earth is immersed when we think about the relation between electicity and magnetissm
derivation of the fourth Maxwell’s eq. is not sastifactory
In 3rd Maxwell Equation make correction of induce end definition as
€= integral (E.dl) becoz electric field is potential gradient not potential density
Then stokes theorem will make appear dA to cancel out both sides